Internal ballistic, or the science of what goes on inside of the gun, is a very complicated topic. This page is not designed to give you a degree in the field but rather to provide some background data to help you understand the subject.
Fr. Frog's Rules of Internal Ballistics
| 1) There ain't no magic
powders! 2) There are no magic cartridge cases! 3) Details! It's in the details. 4) Inconsequential increments are meaningless. 5) Most gun writers are pathological liars. |
Barrel Length - In interior ballistic work this differs from the "barrel length" use in general measurements. It is measured from the face of the muzzle to the base of the seated bullet or base of the case neck.
Bulk Density - The ratio of the weight of a given volume of powder vs. the weight of the same volume of water.
Burning Rate - A arbitrary index of the quickness that burning propellant changes into gas. Burning rate is controlled by the chemical composition, the size and shape of the propellant grains, coatings, and the pressure at which the burning takes place. IMR 5010 powder is very slow burning and Bullseye is fast burning.
For a chart of comparative burning rates for current commercial powders you can click here.
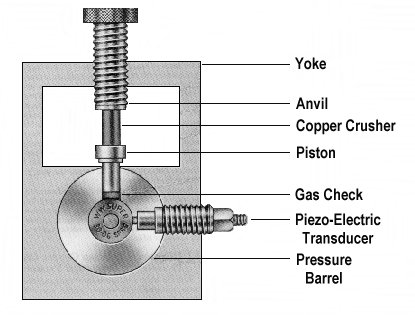
CUP - Copper Units of Pressure. In this pressure measuring technique a hole is drilled in the chamber and a piston fitted that presses on a calibrated copper slug (or crusher). (Some set ups also drill the cartridge case which changes the results compared to non-drilled cases.) The whole assembly is held in place with a yoke. When the cartridge is fired the piston presses on the crusher and deforms it lengthwise slightly. Measurement of the length change is used with a lookup table supplied with each lot of crushers to determine the peak pressure. The total deformation is effected by both the peak pressure and by shape of the pressure curve around the peak pressure. This method tends to give readings slightly lower than the actual peak pressure. A typical reading might be stated as 47,500 CUP which is supposed to be close to the actual average psi measurement. This method has been largely superseded by piezo-electric and strain gauge units which replace the copper slug with a crystal or strain gauge which changes its electrical properties in response to pressure or dimensional changes. Such measurements are stated in PSI. For low pressures a lead crusher can be used and measurements are in LUP.

Typical Dual Measurement (Copper & Piezo-Electric) Pressure Gun
Expansion Ratio - The ratio of the capacity of the powder chamber plus bore (in grains of water) to the capacity of the powder chamber (in grains of water).
Loading Density - The ratio of the weight of the powder charge to the capacity of the powder chamber (case). It is usually expressed as the ratio of the charge weight to the capacity the powder chamber in grains of water. (See below.) Generally, the more fully the powder charge fills the case the more consistent and accurate the load will be. On the other hand if the loading density is too low, (too much free space in the case) it can cause erratic ignition, change in the pressure curve (moving the peak towards the muzzle), or even overly rapid burning ("detonation") of the powder charge. (One reason manuals list minimum or starting loads.)
PSI - Pounds per square inch. It is sometimes seen designated as PSIA. This designation is now used to signify a measurement of chamber pressure taken with a piezo-electric device or a strain gage. Piezo-electric units operate in a similar fashion to the copper crusher units but use a reusable crystal "crusher" that changes its electrical properties in response to pressure. When connected to suitable recording equipment the entire pressure pulse history can be recorded or displayed. The peak pressure recorded by a piezo-electric peak device usually reads higher than the figure determined by the copper crusher method and depending on the cartridge and the pressures involved the differences can range between 3,000 and 15,000 units..
There are also electronic strain gauge units. These work by measuring the expansion of the chamber area on firing by means of device that changes its electrical properties as it changes size. These devices are very sensitive and if one knows the thickness of the walls of the cartridge case and the thickness of the chamber wall, very accurate and detailed information on the pressure curve can be generated.
 |
 |
|
Strain gauge on a dime |
Strain gauge mounted on
rifle |
Piezo (PSI) and strain gauge (PSI) are not directly relatable to copper crusher (CUP) due to the differences in the sensitivity of the copper crusher versus the other methods used to measure the pressure. However, new statistical data analysis suggests that for most cartridges ANSI/SAAMI Maximum Average Piezo (PSI) and Maximum Average copper crusher (CUP) taken in a "standard" barrel can be approximated by the following formula which has an R2 value (a statistical measurement of certainty) of .927.
(1.51586 * CUP) - 17902.0 = PSI
While the relationship is generally within 3Kpsi (it assumes that the CUP was determined using ANSI/ SAAMI standards) one should not rely on this conversion for absolute maximum loads.
Interestingly the correlation between the European CIP CUP measurements and Piezo measurements has an even better correlation with an R2 of .997. The formula for the CIP conversion is
(1.20911 * CIPCUP) - 2806.88 = PSI
The same warning about using this conversion for maximum load work applies to this formula.
|
Comparison of Pressure
Specifications Between Copper Crusher and Piezo |
|||
| Max Average Pressure | Max Probable Lot Mean |
Max Probable Sample Mean |
|
| Copper Units of Pressure (CUP) | 52,000 | 53,300 | 55,300 |
| PSI (Piezo/Strain gauge) | 62,000 | 63,600 | 66,000 |
Powder Chamber Capacity - As with most interior ballistics capacity measurements it is usually expressed in grains of water. It is determined by measuring the weight of water that a fired case from the test firearm can contain with a bullet seated to its normal depth. Note that this varies with different bullets or seating depth as well as the dimensions of the chamber, and the brand of case.
Sectional Density - The is the bullet's weight in pounds divided by its diameter squared.
Charge Weight to Bullet Weight ratio - This is the ratio of the weight of the powder charge to the weight of the projectile.
What Affects What
Among the things that affect the internal performance (pressure and velocity) of a given cartridge & bullet are:
Some Powder Basics
There are basically five types of gunpowder. Black powder, semi-smokeless, pseudo black powder ("Pyrodex"), and smokeless.
Black Powder
In the west it is generally attributed to Roger Bacon or Berthold Schwartz
circa the 1200s, but they basically popularized what had been known for a long
time and did not invent it. It was undoubtedly known to the early Chinese
and Hindu people of India. Some early writings, circa 1300 BC,
from these cultures speak of such a substance though it was used as an
incendiary or a demolition device and not in "firearms." It is
also clear that such a substance was known to the ancient Greeks. The
earliest known use of it as propellant in firearms was by the Arabs circa 1150 in
their war with the Iberians. While the exact proportions have varied over
the years, black powder is basically a finely ground mixture of about 15%
charcoal, 10% sulfur, and 75% potassium nitrate.
Black powder burns so rapidly that it actually explodes even with minimal confinement and unlike modern smokeless powders it is classed as an "explosive". Other than for historical recreational shooting and the manufacture of some types of blank ammunition, black powder is not in general use any more, and with the recent "anti-terror" controls it is getting more difficult to obtain.
Brown Powder
This almost unknown powder was made using under-burnt charcoal and gave
performance not very far below later smokeless powders. Coming at the end
of the black powder age it was superceded after little more than a decade.
Most people have never heard of it. There is a reference on it at https://en.wikipedia.org/wiki/Brown_powder
. There was also a similar high
performance powder that used woodworm dust as the "charcoal
" c.1583, that was used by Spanish aristocracy as it was deemed to
expensive for "common" use
Semi-smokeless
In the late 1800s and early 1900s there was a type of powder known as
Semi-smokeless. This was a mixture of black powder and gun cotton (nitrocellulose)
. Unfortunately the use of raw nitrocellulose made its manufacture very hazardous
and with the advent of modern smokeless powders it was discontinued in the late
1940s.
Pseudo Black Powder (Pyrodex and similar products)
Pseudo black powders such as Pyrodex, Blackthorn 209, Shockley's Gold, and
others are a modern
substitute for black powder and remedy the explosive and fouling problems
of black powder. Due to its chemical make-up, pseudo black powder is
classified as a flammable solid not as an explosive. Pyrodex can be
substituted volume-for-volume for black powder.
Smokeless Powder
The majority of today's small arms smokeless powders are made of either a nitrocellulose base,
referred to as single base powders, and typified by the IMR powders, or of a
nitrocellulose and nitroglycerine mix (usually from 3 to 39 percent), called double base
powders, which include powders like Bullseye, 2400, and Hi-Vel #2.
An early form of smokeless powder was Cordite, which was a double based
propellant made of 65% nitroglycerine, by weight, 30% guncotton and 5% petroleum
jelly, and loaded as spaghetti-like strings of powder. There are
also some special double base ball powders available in non-canister
powders. Double base powders
have a higher energy potential than single base powders. Some modern powders referred to
as "triple base" now incorporate an additional ingredient like
nitroguanidine,
but these, like the double based ball powders are not in wide distribution except military powders and some commercial grade
non-canister powders. They can yield a substantial increase in velocities
while maintaining normal peak pressures as they give a longer, flatter pressure curve. In
addition some manufactures are using "blended powders" for some
of their high performance ammunition.
The grains of modern smokeless propellant powders are made in various sizes and shapes to give the best results in the firearm they are designed to be used in. Powder for the 16" naval cannon has grains almost an inch in diameter and 2½ inches long while typical modern rifle powder has grains only 2/32 or 3/32 of an inch long and maybe a 1/32 of an inch wide. The smaller the grain the faster it burns. Modern powders are available in tubular grains, spherical grains, and flakes.
Most tubular grained powders have a hole through the center of the grain to allow burning to take place from both the inside and outside surfaces. Without the hole, as the grain burned its surface area would decrease and the amount of gas would decrease as the grain burned. Powders of this type, called digressive powders, give peak pressures when the bullet is close to the breech and a low muzzle pressure. By putting a hole down the center of the grain the burning area stays more constant and the maximum pressure point is moved to a point where the bullet has moved further down the bore. These types of powders are called neutral burning.
Another way of controlling the burning rate is with the use of a coating as used with ball powders, which are made with spherically shaped grains. The coating on the powder grain tends to hold back the rate of burning until the coating has burned through. These powders, called progressive burning give a peak pressure at a point in bullet travel even further along. Coating technology is important in small arms powders since without it the grains would sometimes have to be larger than practical.
Much has been made about ball powders being cooler burning than extruded powders, but the fact of the matter is that there really isn't much difference. Flame temperature is very close to the same for all smokeless powders and runs about 3300 degrees F. Ball type powders tend to be from 3200 to 3300 degrees F and extruded powders tend to run 3300 to 3400 degrees F but there is wide variation.
As a technical point of interest, conventional small arms propellant powders have an energy potential of about 178 ft lb per grain of weight. However, in practice this figure is not even closely approached because of various energy losses--such as the energy used in forcing the bullet into the rifling, overcoming bore friction, heating the barrel, and giving the powder gases their high velocity, etc.-- that are inherent and unavoidable. According to The World s Great Rifles, by Roger Ford (1998, Brown Packaging Books, Ltd., London) it is estimated that just one-fifth of one percent of the energy produced when a cartridge is fired goes to rotating the bullet, while friction in the barrel accounts for another three percent, 20 to 30 percent goes to propelling the bullet, 30 percent goes in heat to the barrel, and 40 percent goes in muzzle blast.
Contrary to media myths, smokeless powder is not an explosive but rather a highly flammable solid. (Note that we are talking about smokeless powders here.) As an example, one of the large powder grains used in the 16" naval cannon can actually be lit while held in the hand and then blown out. Even individual grains of modern small arms powders burn very slowly. But, when several grains or a pile of them are ignited together the heat generated by each burning grain makes the adjacent grains burn even faster. A very small pile of smokeless powder burned in the open may seem harmless but the resulting rapid ignition can cause such a rapid build up of heat that a person may not be able to get away fast enough to avoid injury. Inside of a cartridge case the same process happens but on a much shorter time scale.
Bang!
(What happens when the trigger is pulled.)
When you pull the trigger and the primer fires, the intense flame created by the priming compound fills the interior of the cartridge case and ignites the powder charge. The more nearly the powder charge fills the case the less the powder gases generated by the burning powder can expand without doing work and the more the heat generated accelerates the burning process as described above. (Thus a full or nearly full case of powder is more efficient than a partially filled case.) The increasing pressures generated by the burning powder pushes the bullet down the barrel. If the bullet is heavy, tightly held into the neck of the cartridge, or if it is a tight fit in the rifling then the confinement of the powder is accentuated and the burning is proceeds more quickly than if these conditions were not present--in other words you get higher pressures more quickly.
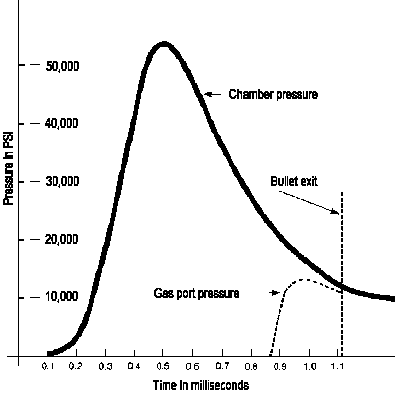
The graph below is a representative pressure curve of a typical cartridge (in this case from the M193 5.56mm cartridge using 846 ball powder). Notice how the peak pressure rises quickly and then tapers off. The location of the peak pressure and the shape of the pressure curve is determined by the burning characteristics of the powder used and the loading density. Slower burning powders tend to have a flatter curve while faster powders a steeper curve.
The gas port pressure curve on this chart shows a critical part of internal ballistics for cartridges used in gas operated firearms. Gas operated weapons are generally tailored to a narrow range of powder burning rates and characteristics. If the port pressure is too low the weapon will fail to function and if to high the weapon may function too forcefully or rapidly causing extraction or cycling problems. A poorly researched change of powder from an IMR type to a ball powder and the subsequent change of port pressure and fouling was what caused all those nightmare stories about the M16 during the early days of the Vietnam war.
Another very good graphical representation of what happens is shown on page 322 of "Hatcher's Notebook", (by Julian S. Hatcher, 3rd edition, June 1962, Stackpole Books, ISBN: 0811707954) but the graph is a little data dense for good reproduction here. It is similar to what is shown above but it is based upon the .30-'06 cartridge, and along with the pressure curve it shows bullet velocity and time of bullet travel.
As can be seen from the above graph, the longer the barrel the more time the powder has to work on moving the bullet, thus you get higher velocities with a longer barrel--all else being equal. However, while not often reached with high powered rifles there is a point at which additional barrel length does not increase velocity, but rather causes a decrease.
As the bullet moves down the bore and the gas pressure behind it decreases there will come a time--with a sufficiently long barrel-- that the bore friction and the air pressure in front of the bullet will equal the pressure behind it. At that point velocity will start to decrease. With the .22 rimfire that point is reached in about 14" - 16" of barrel. Beyond that length no velocity increase occurs, and in fact the bullet can slow down, but the extra length may be useful for other things such as increased sight radius or legal requirements.
If we have to keep barrel length reasonable, the way to get more velocity is to either change the burning characteristics of the powder so it gives higher pressures over a longer time (as is done with the powders in the new "enhanced performance" ammunition now available from Hornady and Federal), or to simply burn more powder by using a bigger cartridge case.
By using a cartridge case with greater capacity we provide for more chamber volume with the same bore volume, thus the expansion ratio (see definitions above) becomes less. As a result, the powder gases have been through less expansion by the time they reach the muzzle and muzzle pressure is higher. As the muzzle pressure is higher, the average pressure along the bore is higher and the bullet has a higher velocity. There is a trade off for this. Because the muzzle pressure is higher, more energy is carried off into the air unused (as flash and muzzle blast) and thus the efficiency of the load (the getting of energy out of the powder charge) is less.
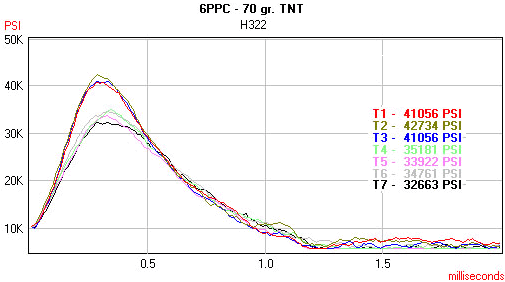
Here is a sample output from PressureTrace for a 6 PPCcartridge. The only difference between all these traces is the first 3 were seated right on the lands. The last 4 were 30 thousands of an inch off the lands. Note the substantially reduced pressure and overall reduction in energy. As the bullet broke it's neck tension and jumped to the lands it provides more expansion room for the gases reducing both the energy and velocity.
The Hacksaw Effect
(Sometimes referred to as "get shorty.")
The often asked the question, "How much velocity will I lose if I shorten my barrel "x" inches?" is tied quite closely to the expansion ratio, although the type of powder also plays a part. Thus there is no clear cut general answer as to just how much velocity is lost per inch of barrel shortening. Rifles with high expansion ratios tend to lose less velocity as the barrel is shortened than do rifles with low expansion ration. Thus a .300 Win Mag will lose more velocity per inch of barrel than say a .30-'06 and it is not uncommon for a smaller cartridge in a long barrel to out perform a big bottle cartridge in a short barrel as some folks found out to their dismay when they chronographed their 22" razzle-dazzle magnums next to their buddies convention calibers with 24" barrels.
Because of the fact that "high velocity" cartridges generally have low expansion ratios (big cases in relation to bore diameter) one can make some generalizations. The chart below will give you some idea of what can be expected if you cut your barrel shorter within the range of 20" to 26". Remember, your mileage may vary from this chart. Note that this chart does not hold true if we are comparing different barrels of different lengths. In that case it is quite possible, due to certain barrel design parameters, for a short barrel to give higher velocity than a longer one with the same ammunition.
| Velocity Range |
Vel change per inch |
| 0-2000 | 5-10 |
| 2000-2500 | 10-20 |
| 2500-3000 | 20-30 |
| 3000-3500 | 30-40 |
There are some "mathematical" methods of computing a fairly close approximation of the actual internal performance (i.e.: chamber pressure and muzzle velocity) of a given combination of cartridge, firearm, bullet, and powder but their details are beyond the scope of this page. The "Powley Computer," a slide rule type device was at one time available and gives rather good results when used with the "IMR" type of powders and cases of similar capacity to the .308 and .30-06. It is based on some mathematically derived "constants" developed at Frankord Arsenal which provide a close approximation to the results derived by some rather complex mathematical gyrations. Several computer-based adaptations of these calculations are available from different sources (such as the rather expensive QuickLoad program) and all suffer from the limitations of being based upon the Frankfort Arsenal model of the .308/.30-06. As far as I know the Powley Computer is no longer available although Powley's code has been privately adapted to computer use by various people. As mentioned previously these computations are based upon case capacities and pressures in the .308 Win & .30-06 range. For cartridges of significantly larger or smaller capacities, or lower pressures, the result will be not be accurate and can frequently be dangerous if you don't understand what is what.. There was a website that allowed you to make your own slide rule computer, but it is no longer active. However, there is an online adaptation of the Powley Computer available at http://kwk.us/powley.html
Mechanical /Electrical Calculation of Internal Ballistics for the End User
Consumer Crusher Systems
Crusher based pressure systems are generally beyond the means of the average
shooter. At one time there was available a "do-it-yourself" pressure measuring device
using a "crusher" type tool. Rather than utilizing a drilled chamber this unit
was mounted on a firearm in place of the telescopic sight and when the firearm was fired
the recoil impulse compressed the crusher which could be measured and compared to a
calibrated table. Unfortunately, the unit was tricky to set up, required very precise
measurements of the firearm's weight, and if memory serves me right worked best when the
firearm was unrestrained in recoil (as in hanging from support wires). It was also only
really suitable for rifles.
Strain Gauge Systems
There are moderately priced electronic strain gauge unit available that
do a better job and allow one to see the pressure curve on an oscilloscope or a
computer screen and
which don't require a special free swinging support. The $500ish PressureTrace
II system and the the
no longer available $800 Oehler Model 43 "Ballistic System"
with its $170 add-on a strain gauge
pressure sensor are examples of this technology.
Strain gauge units with real-time microprocessor compensation such as PresureTrace II have been shown to actually be more accurate than either piezo or crusher measurements. By utilizing certain easily measurable parameters of the chamber wall thickness and cartridge case wall thickness in the firmware and software, the measurements from strain gauge units give results that are accurately given in PSI. (If no compensation is utilized with a strain gauges, the measurements are in arbitrary units, such as "coconuts" as my friend says, which still can be used for comparison readings.
Strain gages have been used in industrial instrumentation for several decades and is fully developed, proven technology. Denton Bramwell, (physicist and statistician with a great deal of test instrumentation experience) recently compared the results of various pressure measurement methods . He used a standard measure of how likely a system will give correct answers called "Sigma E" for comparison. (Smaller Sigma E values are best.)
| System | Sigma E |
| Copper Crusher Fabrique Scientific Peak Strain Meter Commercial piezoelectric Microprocessor compensated strain gauge |
1827 psi 1419 psi 1366 psi 667 psi |
The PressureTrace II unit gives you the actual readings in your firearm, while the Oehler unit converted its measurements to what would probably be obtained by the load in a SAAMI specification test barrel. For the details on the PressureTrace II go to http://www.shootingsoftware.com/pressure.htm.
I have worked with RSI on the development and production of the PressureTrace II unit and I personally use it. It is VERY neat but not inexpensive, running around $500. If you do order one I'd appreciate it if you would let RSI know that I sent you by telling Jim.
NOTE: While you can reliably compare the pressure generated by your handloads with the pressures generated by factory ammunition fired in your gun, or compare the pressures from different handloads in the same gun, strain gauges or recoil based pressure devices do not generate " SAAMI specification" pressure measurements (either PSI or CUP) even thought the results are probably more accurate, because SAAMI specifications currently requires piezo or crusher pressure technology and certain convoluted statistical analysis of the data, as well as requiring that the barrel and chamber be minimum specification to provide "worst case" data. Does it really matter? No.
Case Head Expansion
Some people think it is possible to estimate pressures from cartridge case head
expansion. This has been shown to be incorrect and there is little if any
correlation between case head expansion and pressures. Rather than
reinvent the wheel here visit http://www.shootingsoftware.com/ftp/dbramwell%20july%2019%2004.pdf
for an in depth discussion.
Continuing on...
We know that as pressure goes up, so does velocity. Pressure goes down, so does velocity. If you are worried about pressures, and don't have access to pressure equipment, develop your loads using a soft primer like Winchesters and a chronograph and find the top node or stop when you get flattening or cratering. Then switch to a harder primer and adjust your load to give the node velocity.
While these pressure measuring devices can be very informative for someone with a interest in interior ballistics and the effect that things like different powders and seating depths, most folks who buy these sort of devices don't understand barrel harmonics and velocity nodes. (See the discussion of "load development.") They hope to be able to load all the way up and wring the last foot-second of velocity out of their guns. They forget that the top velocity/accuracy node reachable without signs of excessive pressure (primer flattening/cratering) is the top practical limit for a firearm.
So, what good is being able to "read" pressure? Using PressureTrace II can let you see the effect of burning rates on pressure curves and and the effect of the change of the shape of the pressure curve all of which have an effect on velocity. For many folks it is simply fun to see what is going on. With a highly sensitive unit with a high sample rate like PressureTrace II you can also see the effect of many other things like neck tension, seating depth and powder / bullet / cartridge match. In addition if you are trying to work up a load for a cartridge with little or no published data, a pressure unit can help to keep you safe if you start with data for a cartridge with a similar case capacity and then slowly work up from the lowest pressure loads. If you are working with modified non-standard chamber designs or rifling you can see what is happening and work up safe loads rather than guessing. The loading data for the DMR chamber design for the 6.8 x 43 mm (6.8 SPC) was developed using a PressureTrace II unit.
Rule 1 - Don't do anything stupid.
Rule 2 - For a given load a 3 percent rise in velocity requires a 6 percent rise in chamber pressure.
Rule 3 - For a 3 percent change in case capacity chamber pressure changes by 6 percent. Remember that case capacity varies drastically between brands of cases and that bullet seating depth also changes case capacity.
Rule 4 - Changing ANY component can drastically effect chamber pressure.
Rule 5 - You DO NOT need to wring the last possible foot-second of velocity out of your ammunition--it won't do anything for you. An accurate/moderate velocity load is better than an inaccurate/fast load. (See the external ballistics and load development pages)
Rule 6 - Temperature affects chamber pressure. While the effect differs with each powder, over the range of about 0º F to 125º F most modern commercial powders are fairly stable showing pressure variation of up to ± 3000 psi from loads developed at 70º F. Out side of this range the effect is still there but not as linear.) While most current ball powders handle temperatures changes well some types have exhibited a very non-linear response especially at temperature extremes outside of the above range and can result in catastrophic changes in pressures at temperatures much higher than the original temperature. Loads with any powders should be carefully worked up if their use in extreme temperatures is expected especially if at near maximum (Click here for a chart of temperature effects.)
Rule 7 - Don't do anything stupid.
Unless you are well versed in internal ballistics leave the development of loading data with new powders to the experts with the proper tools, and don't play around with unknown powders. More than one firearm has been destroyed when the wrong powder was used without proper knowledge. As an example, in the 50s and 60s there were a lot of blow ups caused by people trying to use the powder from GI .30-06 blanks in pistols and rifles. What these poor souls didn't realize was that the "EC" powder in those blanks burned so fast that it was also used as a grenade filler. These folks turned their firearms into "grenades" with quite small charges of this powder. By the same token many powders of vastly different burning rates look similar. If it's not in the original can, don't use it!
Leave new load development to the pros and stick with the data in reliable loading manuals.
Bullet Stability
While some may think that bullet stability is an external ballistics issue, it really starts in the bore.
Bullets are stabilized in flight by the gyroscopic effect of their spinning and their spin rate is determined by their muzzle velocity and the rate of twist in the barrel. A badly unstable bullet will actually wobble or tumble in flight resulting in extremely poor accuracy.
The needed rate of twist is effected by the diameter of the bullet, the bullet's weight, and the bullet's overall length. Longer bullets need a faster twist to stabilize. As an example, a 1:12 twist in .30 caliber will adequately stabilized most commercial bullets of up to about 173 grains (depending on the overall length). To use a heavier (longer) bullet or to obtain optimum stability and accuracy with long pointed or boat tailed bullets of that weight requires a 1:10 twist. For best accuracy the slowest twist that will stabilize the bullet should be used. Bullet stability is describe by a number called the Gyroscopic Stability Factor. A stability factor of from 1.25 to 2 is considered "stable." Below that range the bullet is most likely not stable enough for accurate flight. Above that range the bullet may be spinning so fast that it may physically rupture from the forces involved, or minute imbalances that normally would not come to light begin to cause problems.
There is an old formula called the Greenhill Formula that, while it was designed for estimating twists for boat tailed lead core bullets of moderate velocity, does a pretty good job of estimating twist required for flat based bullets under "normal" conditions.
T = Twist in inches
K = Greenhill's constant = 150 (This has to do with the specific gravity of a jacketed lead bullet)
D = Bullet diameter in inches
L = Bullet length in inchesT = (K * D2) / L
Using a 1.35 inch long .308 bullet (173 gr) and crunching the numbers we get about 10.5 (One turn in 10.5", which is pretty close to the 1:10 twist normally used in .30-06 rifles. The twist for the .308 is nominally 1:12 because it was based on the shorter bullet of the150 gr military ammunition from which the .308 commercial round was developed. Most match rifles in .308 have a 1:10 twist to stabilize the 180 and 190 boat tailed match bullets better. The results from the Greenhill formula are on the conservative side--indicating a faster twist than probably needed. That doesn't cause any problems because a little too much stabilization is better than too little.
However, the one big catch with the Greenhill formula is that it does not account for the effects of temperature or muzzle velocity. As temperature or velocity decreases a faster twist is needed to maintain the same level of stability. Colder and thus denser air has a more destabilizing affect than warmer air. A lower muzzle velocity results in a slower rotational speed of the bullet and thus less stability.
As an example of the effect of temperature, the original M16 rifle for the M193 55 gr ball came out with a 1:14 twist which was barely stable at 68 degrees and which was totally unstable below about 40 degrees. They changed to a 1:12 twist to get stability (barely) at colder temperatures. The M855 62 gr round is unstable below about 65 degrees with the 1:12 twist and requires a 1:9 twist to be stable. They went to a 1:7 twist because the M856 tracer round has a very long bullet, but the ball round does just fine in 1:9.
Modern bullet stability calculations are based upon the work of the late Robert L. McCoy who was a ballistician with the Ballistic Research Laboratory at Aberdeen Proving Ground. His work, now used in advanced ballistics programs, accurately takes into account all of the factors involved in bullet stability and accurately describe the bullet's behavior at a given muzzle velocity and twist rate and generates a stability factor for a range of muzzle velocities.
For velocity issues long bullets are more susceptible than short ones. For example the above 173 gr .308 bullet in a 1:12 twist barrel is stable from at muzzle velocities of 4000 f/s down to about 500 f/s . Below that muzzle velocity it becomes unstable. If we turn the design into a VLD bullet with a length of 1.45" (a VLD design has a longer more pointed ogive so the bullet itself gets longer) the bullet is stable for muzzle velocities from 4000 f/s to 3,000 f/s in a 1:12 twist. Going to a 1:11 twist the bullet is stable at muzzle velocities of 4,000 f/s down to about 1150 f/s, and going to a 1:10 twist make the bullet stable at muzzle velocities of 4000 f/s down to about 500 f/s
Another catch with the Greenhill formula is that Greenhill assumes that the bullet's specific gravity is 10.9 (a lead cored jacketed bullet). For other bullet construction such as a steel core you need to apply a fudge factor by determining the bullets specific gravity. The formula would be:
Twist = [Square Root (10.9 / specific gravity of the new bullet)] * twist derived for a lead core bullet
You can determine the specific gravity of a bullet thusly:
1) Suspend the bullet at its balance point from the pan of a
scale.
2) Weight the bullet.
3) Place a container of water under the scale so the bullet hangs fully in the
water and weigh the bullet.
4) Subtract the weight obtained in step 3 from the weight obtained in step 2
5) Divide the weight obtained in step 2 by the difference obtained in step 4.
As an interesting exercise you can also determine the spin needed in mediums other than air under "standard conditions" by multiplying the spin for air by the square root of the number obtained by dividing the density of the medium in question by the density of air. As an example water is about 900 times as dense as air: 900 / 1 = 900 and the square root of 900 is 30. Thus you need a twist 30 times as fast to stabilize a bullet in water.
Sharp eyed reader may note that the McCoy stability computations are based upon muzzle velocity. This is the case because the rotational speed decays much more slowly than velocity decay. Most of the research in this area was done by the Ballistics Research Lab at Aberdeen Proving Ground and Picatinny Arsenal on artillery projectiles which have narrow driving bands that are engaged by the rifling rather than full body length rifling engraving on the bullet as with small arms projectiles. Thus there are some approximations made on spin decay for small arms projectiles. For the M80 147 gr 7.62 NATO bullet at 2750 f/s which has been studied and investigated thoroughly, the approximate spin decay at range is linear as shown below. The decay rate probably holds true for other small arms cartridges.
| Range | Muzzle | 100 | 200 | 300 | 400 | 500 | 1000 |
|
Percent of spin remaining |
100 | 98 | 96 | 93 | 91 | 89 | 75 |
| Bullet RPM | 198,000 | 194,000 | 190,000 | 184,000 | 180,000 | 176,000 | 148,500 |
To email me click here
| Ballistics Main Page | External Ballistics Page | Zeroing Page | Terminal Ballistics Page |
| Rifle Power Page | Misc. Questions |
| Back to Fr. Frog's Home Page |
Disclaimer
As far as I know all the information presented above is correct and I have attempted to insure that it is. However, I am not responsible for any errors, omissions, or damages resulting from the use or misuse of this information, nor for you doing something stupid with it. (Don't you hate these disclaimers? So do I, but there are people out there who refuse to be responsible for their own actions and who will sue anybody to make a buck.)
Updated 2018-12-26