Miscellaneous Questions #2

This section continues the discussions of various ballistics and shooting related topics as requested by correspondents. If you have a question you have been trying to find an answer to (keep 'em ballistics or shooting related--see your minister for the mysteries of life) email me by clicking here and I'll do my best to find the answer for you and if it is of general interest, publish it here. If you can contribute additional input to one of the answers I'd would appreciate hearing from you too.

A. The answer to that question depends upon whether we are talking about practical firearms or laboratory curiosities.

The theoretical maximum velocity attainable from normal commercial propellant powder and "conventional" loading densities is limited by the maximum velocity of expanding powder gases. Under ideal conditions this is stated as somewhere between 5700 f/s and 6000 f/s , and in conventional small arms between 4000-5000 f/s, by most authorities. Using specialized "solid propellants" the upper limit is theoretically about 13,000 f/s but at pressures way beyond practical.

Even under ideal laboratory conditions the maximum velocity attainable with standard propellant powders is limited by two factors: 1) A substantial portion of the energy derived from the burning powder is used up in accelerating the mass of gas behind the projectile, and 2) regardless of the amount of powder used energy transfer to the projectile can take place only at velocities that are less than the escape velocity of the propellant gases. Since the bullet cannot travel faster than the gases pushing it this sets a velocity ceiling. While raising pressures by burning huge amounts of powder can achieve some spectacular velocities there comes a point of diminishing returns, because most of the additional energy must be used to accelerate the greater mass of propellant gases produced.

Aberdeen Proving Ground reached close to 9000 f/s using a .60 cal smooth bore gun and using 720 gr (!!) of IMR 4895 and a 113 gr projectile and they believed that the theoretical maximum velocity in that "gun" would be about 10,000 f/s. The all time record for a conventional solid propellant gun (as opposed to light gas guns, etc.) is believed to be held by the people at the Canadian Armament Research and Development Establishment (CARDE). In the early 1960s they used an 81.3mm smoothbore gun with a 95 caliber length barrel to reach the blistering muzzle velocity of 9154 f/s but I don't have any information on the projectile or the type of powder used. (A velocity of 9153 feet per second was supposedly achieved in 1938 by a German experimenter named Langweiler, firing a special 8 mm round using a 1 meter (39") barrel. The bullet weighed about 3.85 gr and the propelling charge was 170 gr of an unspecified powder designed to give a larger burning surface to the grains. The maximum pressure in the gun was listed as 176,500 psi. The reported velocity is generally considered suspect due to the limitations of the powder gas velocities and to the primitive velocity recording done via a ballistic pendulum.)

In more conventional firearms the .220 Swift is capable of launching a 40 gr bullet at around 4380 f/s from a 26 inch barrel which is fast in anyone's book and is probably the "commercial" rifle ammunition record. In handguns, velocities close to 3000 f/s have been achieved using a single shot pistol with such commercial rounds as the .222 Remington and 40 gr bullets, but I'm sure that someone out there has chambered a Contender in .220 Swift or something equally insane.

Some rifle experimenters have reported velocities around 5300 f/s using huge powder charges and light weight bullets. One example was a .378 Weatherby necked to .30 caliber and firing a 30 gr "pellet." Reportedly projectiles of down to about 3 gr were also used. As you might expect the barrel only lasted for a couple of shots. Another cartridge known as the .316 (some sources say ".416") Gerlich (designed in the late 1930s by Hermann Gerlich) is reported to have achieved 5,325 f/s from a 34 inch barrel with a 118 grain bullet on top of 146 grains(!) of IMR4895 and ordnance test reports indicate that velocities of up to about 5700 f/s may have been achieved using a squeeze bore design in which the bullet starts out at one diameter and is squeezed down to a smaller diameter at the muzzle. Most of the Gerlich rounds used a bullet that started out at .316" and exited the muzzle at .240".

For non conventional "firearms," laboratory devices utilizing exotic gases or large charges of unconventional powders as a propellant, and evacuated bores and target chambers have yielded velocities of 25,000 f/s and higher using projectiles as heavy as 237 gr and a 20 foot long evacuated bore and target chamber. (The August 2003 American Rifleman had an interesting article on these "guns.") Electromagnetic "rail guns" have also been achieving very high velocities, up to 26,000 f/s or more, using projectiles weighing up to 16 lbs. In a more practical vein The US Army's "Miramar Gun B" rail gun fired a 2.30 lb projectile at over 11,150 f/s, at sea level in the atmosphere and that was only at about 80 percent of capacity. I'll leave it to you to figure out the KE.

In 2007 BAE Systems delivered a 32 megajoule launcher to the Office of Naval Research (ONR) Electromagnetic Launch Facility. On 31 January 2008, test firing began with this launcher. The rail gun was fired at 10.64MJ (megajoules) and the 7 lbs. (3.2 kg) test projectile attained a muzzle velocity of 8,268 fps (2,520 mps). In 2010 the same gun was successfully fired at 33 MJ and a 40 pound projectile reached a reported 8500 fs. This equates to some 44.5 million ft lb if I did the math right. They are supposedly working on a 60+ megajoule gun that should come close to doubling the velocity and give nearly 140 million ft/lb. The navy is getting ready (2018) to field a 35MJ rail gun that launches a 23 pound projectile at close to 8500 fs

The practical velocity championship for current "working" ammunition should probably go to either the M829 APFSDS-T (Armor Piercing Fin Stabilized Discarding Sabot-Tracer) 120mm rounds as fired by the M1 Abrams tank, or to the Soviet equivalents. The original M829 threw a 9.41 pound (that's 65,870 grains), 1.06" diameter, 24" long, depleted uranium dart at 5480 f/s! The A1 version fired a 10.78 pound dart at 5170 f/s and the current A2 version throws a slightly longer (30") but skinnier (.8") 10.85 pound dart at 5512 f/s. (For you hand loaders, operating pressures of the M829 series are between 74K psi and 96K psi.) The M865 TPCSDS-T (Target Practice Cone Stabilized Discarding Sabot with Tracer) training round throws a 7 pound aluminum dart at 5577 f/s. (This round has a MUCH shorter maximum range than the M829 and can thus be safely fired on most tank ranges.) There is also a new US M829A3 round that reportedly launches a 22.2 pound (!) dart at 5200+ f/s although velocities as high as 5600 f/s have been reported in some publications. (Even at "only "5200 f/s that's 9.2 MILLION foot-pounds of KE!)

The Russian 125 mm equivalents of the US rounds reportedly launch their projectiles at close to 5900 f/s but their terminal performance is still inferior to the US rounds. Several years ago the Ukrainians showed off a prototype of a longer 125mm gun, called Vitiaz, and it reportedly launches its 5 kg projectile at 6660 f/s but these specifications are not verified and are suspect.

Q. If you were limited to just one rifle for use on all kinds of game, what would you recommend?

A. This is one of those questions that can break up marriages! However, if I was going to be limited to just one rifle for hunting all over the world my choice would be a bolt action .30-'06 (known in other places as the 7.62 x 63) with a 24" barrel with a 1:10 twist, and the best quality scope of about 4 power or a 1.5 x 6 variable, that I could buy. Why? because of its great versatility. Factory ammunition is available world wide in bullets weights from 93 grains all the way up to 220 grains and higher with both standard and premium bullets, and with reloading even heavier bullets are available. (The .308 is pretty much limited to 200 gr bullets because of its short overall length. A .308, however, would suffice if you had no interest in the heavier game.) Inexpensive GI practice ammunition is still generally available too.

The .30-'06 is powerful, and can come fairly close in performance to some of the .300 magnums, especially when using the "enhanced performance" ammunition now available from several makers. While it is not an elephant, buffalo, or moose gun, it has, countless times, killed them all very cleanly and satisfactorily. It is not a "varmint" cartridge but it can be used very handily in that roll. It shoots flat enough for use at really long ranges yet it is easy on the shoulder. In an 8½ or so pound rifle (sighted and slung) it is easily managed and this leads to more practice shots being fired. It is an inherently accurate cartridge, all of its secrets have been pretty much learned by now, and its case life and barrel life are very good, something that can't be said about some of the magnums.

The only possible negative point that I can see is that it might be prohibited in some countries as a "military" caliber, as could be the .308. However, there is a nifty workaround available. What a friend of mine has done is to have his .30-'06 rechambered to the .30-'06 Ackley Improved (a very simple and inexpensive job) and marked ".30 Ackley" on the barrel. It will fire standard .30-'06 ammo just fine (Shh! Don't tell those customs agents!) and with the cases thus fire formed it can be reloaded to .300 Mag performance levels with standard powders. Talk about a "rule beater!" As many famous hunters have said, "If you can't do it with a .30-'06, you probably can't do it.

Q. Why do some barrels give higher velocity than others of the same or longer length?

A. There are a lot of factors that can influence a barrel's performance. While it is often believed that it is the "smoothness" of the barrel, an extremely smooth bore surface will actually produce a small velocity loss (50 f/s). This is counter-intuitive for most people, but it relates directly to the fact that gas pressure does not build up as quickly behind a bullet that can slide very easily down a bore.

One thing that can increase velocity is a bore that tapers from the breech to the muzzle. The taper must be along the lines of .001 inch per 28 inches of barrel length but this seemingly slight taper can have a profound effect on the time/pressure curve. (Remember, that ".001 inch per 28 inches of barrel length" is just a way of expressing the angle of taper. The actual barrel length doesn't affect what happens if the angle of taper is the same.) The bore at the chamber end should start within ± .0002" of nominal for that caliber. (For example, a .308 caliber barrel should measure between .3078 and .3082 just ahead of the throat, and preferably between .3080 and .3082.)

With a tapered bore, the peak pressure spike is lowered while the descending branch of the pressure curve is raised. (See my internal ballistics page for an explanation of the pressure curve.) This represents an ideal situation, as more of the pressure is being distributed down-bore behind a bullet that is engaging very solidly into the rifling during the entire time that it is in the bore. If one handloads, one can take advantage of the increased efficiency and increase the charge weight accordingly. This will typically result in a net overall gain of 5-10 percent additional velocity that would not be possible at identical pressures in a straight-bored barrel.

Slightly over-sized barrels can also give increased velocity over nominally or tightly configured non-tapered custom barrels. Another issue which can contribute to higher than "normal" velocities is shallower-than-normal lands, which accounts for the reason that Shilen barrels are often regarded as being "faster" than Harts.

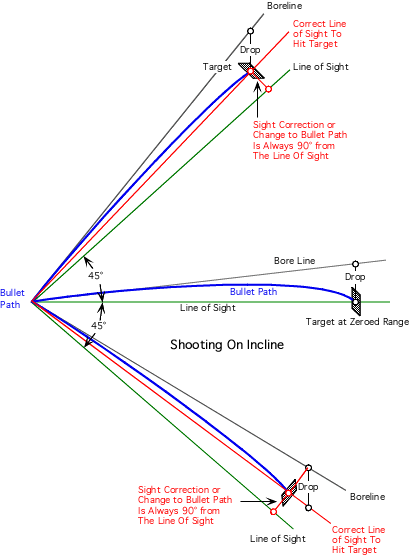
Q. What effect does shooting at an up-hill or down-hill angle have on bullet trajectory?

A. When you shoot up hill or downhill your point of impact will always be higher than expected. When shooting uphill or downhill the true drop of the bullet measured at any angle from the muzzle changes very little from the true drop when fired horizontally even at steep angles. (The term "drop" as we use it is always measured in a vertical direction at the target and is the vertical distance between the line of departure (or bore axis) and the bullet's path.) However, the the height of the bullet's path in reference to the shooter's line of sight does change significantly. The effect can be seen in the graphic below.

You can compute the difference in point of impact when firing at an angle with some ballistics software or you can manually compute the difference if you know the true drop at the range in question (often included in ballistics tables) with the table below.

Angle (deg)	Increase in Bullet Path Height (in)	Angle (deg)	Increase in Bullet Path Height (in)
± 5	.004 d	± 35	.181 d
± 10	.015 d	± 40	.234 d
± 15	.034 d	± 45	.293 d
± 20	.060 d	± 50	.357 d
± 25	.094 d	± 55	.426 d
± 30	.134 d	± 60	.500 d
d = true drop at given range

Another thing that messes up most folks even more when shooting up-hill or down-hill is that they don't know anything about the trajectory of their projectile to begin with. This makes hitting anything problematical whether shooting horizontally or at an angle.

A. If we ignore bedding (the fitting of the barrel to the action and stock) the most important qualities are the dimensions and concentricity of the throat and the bore, surface quality of the throat, consistency of twist throughout the length of the barrel, lack of stresses in the barrel walls and their concentricity, and the absence of significant dimensional anomalies (tight spots, loose spots, reverse taper to the bore) that cause the gas seal to be interrupted or damaged. In addition, the condition and the concentricity of the crown (the muzzle opening) has a great affect on accuracy.

A. Fluting provides a slight reduction in weight but little else. (Although some folks think it looks "neat.") It does not increase stiffness or accuracy, nor does it provide any meaningful heat dissipation. In fact the process of cutting flutes can distort and ruin a barrel if not done right.

If you take two barrels of the same shape, and one is larger diameter and fluted, while the other is of a smaller diameter and unfluted, the larger diameter fluted barrel will be stiffer. But, if we take two barrels of identical weight and contour and flute one, it will be much less stiff than the unfluted barrel. As far as cooling is concerned, for there to be an significant difference in the dissipation of heat the barrel would have to have 4-6 inch fins radiating from it, preferably made from a heat conducting metal such as aluminum. Flutes simply will not make a practical difference, though technically any increase in surface area does promote faster cooling. However, they do look "cool."

Q. How do you determine the rifling twist needed to stabilize a given bullet?

A. The needed rate of twist is affected by the diameter of the bullet, the bullets weight, and the bullet's overall length. Longer bullets need a faster twist to stabilize. As an example, a 1:12 twist in .30 caliber will adequately stabilized most commercial bullets of up to about 175 grains. To use a heavier (longer) bullet or to obtain optimum stability and accuracy with long pointed or boat tailed bullets of that weight requires a 1:10 twist. For best accuracy the slowest twist that will stabilize the bullet should be used.

Modern bullet stability calculations are based upon the work of the late Robert L. McCoy who was a ballistician with the Ballistic Research Laboratory at Aberdeen Proving Ground. His work, now used in advanced ballistics programs, accurately takes into account all of the factors involved in bullet stability and accurately describe the bullet's behavior at a given twist rate and generates a stability factor. A stability factor of from 1.25 to 2 is considered "stable."

There is an old formula called the Greenhill Formula that, while it was designed for estimating twists for boat tailed lead core bullets of moderate velocity, does a pretty good job of estimating twist required for flat based bullets under "normal" conditions.

Using a 1.35 inch long .308 bullet (173 gr) and crunching the numbers we get about 10.5 (One turn in 10.5", which is pretty close to the 1:10 twist normally used in .30-06 rifles. The twist for the .308 is nominally 1:12 because it was based on the shorter bullet of the 150 gr military ammunition from which the .308 commercial round was developed. Most match rifles in .308 have a 1:10 twist to stabilize the 180 and 190 boat tailed match bullets better. The results from the Greenhill formula are on the conservative side--indicating a faster twist than probably needed. That doesn't cause any problems because a little too much stabilization is better than too little.

However, the one big catch with the Greenhill formula is that it does not account for the effects of temperature or muzzle velocity. As temperature or velocity decreases a faster twist is needed to maintain the same level of stability. Colder and thus denser air has a more destabilizing affect than warmer air. A lower muzzle velocity results in a slower rotational speed of the bullet and thus less stability.

As an example of the effect of temperature, the original M16 rifle for the M193 55 gr ball came out with a 1:14 twist which was barely stable at 68 degrees and which was totally unstable below about 40 degrees. They changed to a 1:12 twist to get stability (barely) at colder temperatures. The new M855 62 gr round is unstable below about 65 degrees with the 1:12 twist and requires a 1:9 twist to be stable. They went to a 1:7 twist because the M856 tracer round has a very long bullet, but the ball round does just fine in 1:9.

For velocity issues long bullets are more susceptible than short ones. For example the above 173 gr .308 bullet in a 1:12 twist barrel is stable from at muzzle velocities of 4000 f/s down to about 500 f/s . Below that muzzle velocity it becomes unstable. If we turn the design into a VLD bullet with a length of 1.45" the bullet is stable for muzzle velocities from 4000 f/s to 3,000 f/s in a 1:12 twist. Going to a 1:11 twist the bullet is stable at muzzle velocities of 4,000 f/s down to about 1150 f/s, and going to a 1:10 twist make the bullet stable at muzzle velocities of 4000 f/s down to about 500 f/s

Another catch is that Greenhill assumes that the bullet's specific gravity is 10.9 (a lead cored jacketed bullet). For other bullet construction such as a steel core you need to apply a fudge factor by determining the bullets specific gravity. The formula would be:

Twist = [Square Root (10.9 / specific gravity of the new bullet)] * twist derived for a lead core bullet

1) Suspend the bullet at its balance point from the pan of a scale.
2) Weight the bullet.
3) Place a container of water under the scale so the bullet hangs fully in the water and weigh the bullet.
4) Subtract the weight obtained in step 3 from the weight obtained in step 2
5) Divide the weight obtained in step 2 by the difference obtained in step 4.

As an interesting exercise you can also determine the spin needed in mediums other than air under "standard conditions" by multiplying the spin for air by the square root of the number obtained by dividing the density of the medium in question by the density of air. As an example water is about 900 times as dense as air: 900 / 1 = 900 and the square root of 900 is 30. Thus you need a twist 30 times as fast to stabilize a bullet in water.

A. Before we can answer that question, a brief discussion of small arms "effectiveness" is in order. When talking about the effectiveness of any small arms system, it should be noted that the military looks at effectiveness in a different light than the law enforcement or civilian user. The police officer or civilian is interested in the immediate termination of the actions of the individual shot--the proverbial "instant incapacitation." The military on the other hand is primarily interested in creating a wound that will make the casualty combat ineffective, require medical treatment and hopefully the use of several other enemy troops to help the individual who was hit.

Thus, the military considers that an effective hit is one that delivers approximately 53 foot pounds (some sources say 35) of energy to the target rather than one that instantly shuts down the target. A good riotgun with a load of #4, #1, or 00 buck can provide several, if marginal, hits on a full length human target at 80 to 100 yards when directed with a good set of sights. (The typical "bead" front sight only is next to useless.) If viewed in the military perspective, the 12 gauge riotgun firing buckshot can be "effective" on individual targets out to 100 yards. One needs to get much closer if one wants anything like "instant incapacitation."

At normal distances, if one is to believe the media, a charge of buckshot from a typical riotgun spreads out to about six feet in diameter at the muzzle. It then roars down range with an effect just slightly less than a tactical nuclear device, destroying everything in its path. On the other hand, some say that the riotgun is only a very short range weapon with limited use and effectiveness. The truth, it turns out, is somewhere in between.

First of all, consider the fact that shot typically spreads 1" for each yard of range. (Your results may vary but you'll be close to this.) Thus, it is quite easy to totally miss a nearby target unless you aim at it.

Second, past about 30 to 35 yards (again your results may vary but you'll be close) your shot pattern may be so large that only a few, if any, pellets will hit the target.

Third, we need to consider just what is going on when you fire a round of buckshot. Less anyone thinks that marginal hits from only one or two pellets of 00 buck will effectively turn off an attacker, consider what is actually striking the target. A pellet of 00 buck is essentially a 54 grain, .33 caliber projectile that is traveling between 1100 and 1300 feet per second depending on the load. This puts the effectiveness of each pellet of 00 buckshot somewhere between that of the .32 ACP and .380 ACP cartridges, neither of which most folks want to put their life on the line with. The table below compares some common buckshot loads.

Shot Size	Pellet Diameter (in)	Pellet Weight (gr)	Velocity (f/s)	Individual Energy (ft lb)	Number of pellets in loading	Total Weight (oz)	Total Energy (ft lb)
000	.36	70	1265	250	8 in 2¾"	1.3	2,000
00	.33	54	1295	200	9 in 2¾"	1.1	1,810
0	.32	48	1200	155	12 in 2¾"	1.3	1,860
1	.30	40	1215	130	16 in 2¾"	1.5	2.080
4	.24	20	1260	70	27 in 2¾"	1.2	1,890
#6 Shot	.11	1.9	1290	7	280 in 2¾"	1.25	1,970
.32 ACP	.31	71	900	130	-	-	-
.380 ACP	.35	90	950	190	-	-	-
38SPL +P	.35	158	890	280	-	-	-

Fourth, penetration is an important part of the incapacitation process. (See my terminal ballistics page.) Shot, because of its spherical shape (and thus low sectional density) has inherently poor penetration compared to a conventional bullet, especially if deformed by intervening material. (#4 buckshot is especially known for this problem.) The so-called "premium" buckshot loads with their hardened and/or plated pellets generally give the best performance because the pellets don't deform as much.

If one uses the larger sizes of buckshot (1 or larger) and places the majority of pellets (75%--6 or more of 00 buck) well centered on the target the riot gun can be quite effective up to the limits of its patterning--but it is not failure proof. If the target is covered with intervening material such as heavy clothing things may not go as you expect. Past the 30-35 yard range you will need to switch to slugs which will extend your effective range out to around 100 yards or so assuming you have a set of sights (front and rear) on your shotgun.

A. Nominally the gauge number is the number of lead balls of bore diameter than weigh one pound. See table below.

Gauge	Bore Diameter (in)	Gauge	Bore Diameter (in)
1	1.669	16	.662.
2	1.325	20	.615
4	1.052	24	..580
8	.835	28	.550
10	.775	32	.501
12	.729	.410*	.410
14	.693
* The equivalent gauge would be somewhere around 64

As far as I know all the information presented above is correct and I have attempted to ensure that it is. However, I am not responsible for any errors, omissions, or damages resulting from the use or misuse of this information, nor for your doing something stupid with it. (Don't you hate these disclaimers? So do I, but there are people out there who refuse to be responsible for their own actions and who will sue anybody to make a buck.)